Mathematics of the Ancients

I. Mathematics from Mesopotamia

A. Sumer

1. The Sumerians developed the first writing system, called cuneiform, around 3,000 B.C. The first numbers were written in cuneiform.
2. As Sumerian society became more complex, trade flourished and government grew. Mathematics became necessary to keep track of trade and with growing administrative problems.

B. Akkad

1. Around 2,300 B.C., the Akkadians (another Mesopotamian people) conquered Sumer. The Akkadian contribution to mathematics was introducing the abacus. With it, methods of addition, subtraction, multiplication, and division were introduced, although done rather primitively. The Akkadian influence to mathematics was short-lived. The Sumerians revolted and were back in control by 2,100 B.C.

II. Mesopotamian Masters of Mathematics

A. The Babylonians

    

1. Around 2,000 B.C., a Semitic people came out of what is now Saudi Arabia, and conquered the Sumerians. These people became known as Babylonians, named after their capital city, Babylon.
2. Babylonians were the true Mesopotamian geniuses in mathematics.
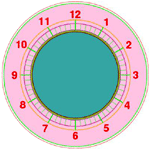
3. Babylonians developed counting on a sexagesimal system – that is, a base 60 system of counting. Today, we have a base ten system of counting. This Babylonian base 60 counting has existed for over 4,000 years, and we still use it today when we tell time. Babylonians divided the day into 24 hours, the hour in to 60 minutes, and the minutes into 60 seconds.
4. Having a base 60 system of counting meant the Babylonians used 59 different symbols for their writing. Interestingly, their numbers are all variations of the construction of only two symbols. In base ten, we have nine numbers– 1, 2, 3, 4, 5, 6, 7, 8, and 9. The number, 10, is merely just the first number again with a placeholder zero. On a side note, the symbol for zero, 0, would not be invented for hundreds of years, until the Indians started using it. It is uncertain just exactly what was used before the zero was invented, although the Babylonians used two wedges (looking like quotation marks) to denote a placeholder. Later, they used a symbol that looked like a hook.
5. Base 60 is considered to be superior to base ten in some ways. It is easier to work with, especially when dealing with fractions. Think of all the factors of ten – 1, 2, 5, 10. Now think of all the factors of 60 – 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. Therefore, it’s much easier to make a fraction out of 60, say 20/60, which can easily be reduced into an equivalent fraction. Think of a clock. The parts of the clock can all easily be expressed as fractions. For example, six minutes is 1/10 of an hour. Neat, huh?
6. Here’s an example of how easy it is to work in base 60. Say you have to do four math problems in one hour. How much time will it take to do one problem? It’s simple: since four easily goes into 60, the answer is it will take 15 minutes to do one problem. The division was clean with no remainders, no decimals. Now, let’s say we’re using a clock which functions using base ten. Instead of minutes, let’s use the made-up word, decits. In this base ten system, it takes ten decits to make an hour. So, it you’re asked to do four problems in one hour, how much time will it take to do one problem? The answer is not as clean. It takes 2.5 decits to do one problem. Since so many more numbers will divide into 60, it’s easier to work with than base ten.
7. Babylonians excelled at making mathematical tablets. Two tablets found at Senkerah near the Euphrates River give the squares of numbers up to 59 and cube roots up to 32.
8. Babylonians invented place value or a positional system for numbers. Neither the Sumerians nor the Akkadians had this.
9. Babylonians became so advanced they were able to create tablets that dealt with geometry, linear and quadratic equations, and astronomy.

III. Mathematics from Egypt

A. Practical Mathematics

    

Video: Egyptian Number System

Video: Telling Time in Ancient Egypt

1. Mathematics in Egypt probably began around 3,000 B.C. Theirs was a practical sort of mathematics. Egyptians applied mathematics which affected their daily lives, and were not concerned with the abstract. Egyptians were concerned with practical things, like knowing the depth of the Nile, the weight of a sack of grain, and accurate measurements for building. Egyptians used mathematics for their calendar, and were the first to create a 365-day calendar.
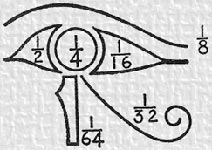
2. Egyptian numerals were poor for multiplication and division. They devised methods of multiplication and division by using clever tricks of addition and subtraction. Egyptians did use fractions, and believed that some fractions had mystical properties. The Eye of Horus, for instance, had six separate fractions representing the six separate parts to the eye.
3. An example of Egyptian fractions is found on a tablet called the Akhmim Wooden Tablet. It seems to show fractions being used to divide units of grain.
4. Another famous mathematical artifact from Egypt is the Rhind Papyrus, written by the Egyptian scribe, Ahmes, around 1650 B.C. The Rhind Papyrus makes reference to pi. It contains mathematical problems and their solutions. Here’s a famous example: Seven houses contain seven cats. Each cat kills seven mice. Each mouse had eaten seven ears of grain. Each ear of grain would have produced seven hekats of wheat. What is the total of all these?

IV. Mathematics from Ancient India

A. The Indus Valley Civilization

Video: Ancient Indian Math

1. The first evidence of mathematics in India came from the Indus Valley Civilization, which existed from 2,500 B.C. to 1,750 B.C. One of the cities from this civilization was Harappa. The Harappans had a standard system of weights, which must have been used in trade. These various stones could be weighed counter to an object for sale to determine the item’s worth. Harappans also had a standard measuring system for length. A small rod, called an Indus Inch, was thought to be used to measure the length of items. It is equivalent to a modern 1.32 inches.

B. The Vedas

Video: Vedic and Jain Math

1. The Vedas are the four holy books of the Hindu religion. Although they are religious books, the Vedas contain information on mathematics and science.

C. The Sulbasutras (Circa 1,000 – 200 B.C.)

1. The Sulbasutras are appendices to the Vedas. They were written for Vedic priests to correctly construct religious altars. Precise instructions and measurements are given, including the discussion of creating a right triangle. From this, it seems ancient Indians were at least partially aware of geometric principles.

D. Brahmi Numbers

1. Around 300 B.C., a series of nine numerals were created called the Brahmi numerals. These numerals evolved over the centuries, and modified by Arabs. The West inherited these numbers from the Arabs to become our modern 1, 2, 3, 4, 5, 6, 7, 8, 9.

E. Jainism-Indian Mathematics Takes a Huge Leap Forward

1. Jainism is an offshoot of Hinduism, and probably first appeared around the sixth century B.C.
2. Jains were interested in mathematics. By 150 B.C., Jain mathematicians were working on number theory, arithmetical operations, geometry, fractions, simple equations, permutations, and combinations.

V. Mathematics from Ancient China

A. The Shang Dynasty 1,500 to 1,050 B.C.

Video: Chinese Numbers

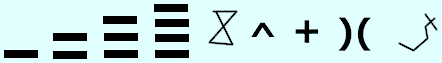
The shells or bones were heated, and the cracks that appeared were considered to be Shang Di’s answers to these questions. From these shells or bones, called Oracle bones, it appears the Shang had a base ten system with place values.

1. The first evidence for number symbols in ancient China appears with the Shang Dynasty. Shang diviners carved symbols on scraped tortoise shells or flat cattle bones to ask questions of their supreme god – Shang Di.

B.Mathematics Shrouded in Myth

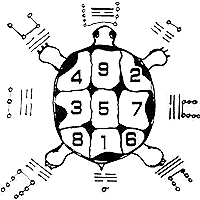
1. Chinese mythology holds an older tradition for mathematics. A legendary emperor, Emperor Yu, received a holy gift from a tortoise living along the Lo River. The gift was in the form of diagrams called Lo Shu. One diagram, called the Magic Square, was thought to have magical properties and led to the dualistic theory of the Yin and Yang. Yin represented even numbers, and Yang represented odd numbers.

 

C. Evidence of Ancient Mathematics?

1. Mostly, the evidence for ancient Chinese mathematics is sketchy. The oldest book of mathematics in China is from 180 B.C. It was called the Suan Shu Shu (A Book on Arithmetic), and was written on bamboo strips. Scholars only have parts of this book, the rest being lost in time.
2. The oldest mathematical text from China scholars have in its entirety is called, Zhou Suanjing (Zhou Shadow Gauge Manual), which was written between 100 B.C. and 100 A.D. It is a book on astronomy showing how to calculate the positions of the heavenly bodies.

D. The Importance of the Calendar

1. Calendars were very important to the ancient Chinese. Beyond giving dates and times for seasons, calendars were seen as a symbol of the emperor’s rule. A new emperor would change the calendar to show his control over time and his link with the heavens. Ancient Chinese calendars showed the positions of the heavenly bodies, which were more than just planets and stars. They had religious significance to the ancient Chinese. When an emperor controlled the calendar, which showed the planet’s positions, he showed his command over the heavens.
2. For example, the Han emperor, Wu-ti, had a new calendar made for his rule. Mathematician, Luoxia Hong, created a new calendar for Wu-ti, which was based on a 19-year cycle.

VI. Mathematics from Ancient Greece

A. Geometry

Video: Greek Mathematics vs Egyptian and Babylonian Mathematics

Video: Greek Mathematician

1. It is hard to say exactly when the ancient Greeks first developed numbers and used them for basic arithmetic. Greek mathematics would really take off (and influence the western world ever since) with the philosophers known as the pre-Socratics. You may recall Thales (624-548 B.C.) was the first pre-Socratic philosopher. Mathematics, science, and philosophy were one and the same to the ancient Greeks, so it is not surprising that philosophers were the first Greek mathematicians.
2. All ancient Greek mathematics was based on geometry. Even when discussing number theory, the Greeks did so on terms of how numbers appear in geometry. Take the number pi (3.14…), for instance. The Greek discovery of pi was done through geometry. Greeks noticed that whenever they divided the diameter of a circle into its circumference, the result was always three point something, or pi. They saw that no matter how large the circle, the diameter was always a little more than one-third of the circumference.

B. Pythagoras and the Pythagoreans

  

1. Pythagoras of Samos (560-480 B.C.) was a philosopher and religious leader. He founded a philosophical and religious school in Croton. The mathematical theories developed there, are always attributed to Pythagoras, because it is unknown whether he or his students were the true creators.
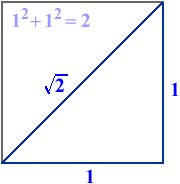
2. Pythagoreans believed everything in the universe could be reduced to number relations. As you know, Pythagoras is most famous for describing the relationship between the squares of the base and height of a right triangle with the square of its hypotenuse. Interestingly, it was none other than this theory, which would rock the Pythagorean world to its knees.
3. Remember, Greek mathematicians (and the Pythagoreans) expressed all their mathematics through geometry. They believed that whole numbers and their ratios could account for all geometric properties. But, the Pythagoreans discovered a major problem. Take an isosceles right triangle. Say the base and height are one inch. The Pythagorean Theorem says the base squared plus the height squared equals the hypotenuse squared. So one squared plus one squared equals the hypotenuse squared.  One squared is one. So, you get one plus one equals the hypotenuse squared. Finally, you’re left with two equals the hypotenuse squared. To find the hypotenuse at this point, you must find the square root of two. When the Pythagoreans first did this problem, it probably made them scream in frustration, because what the fiddle is the square root of two? They didn’t know. The square root of two is an amount which cannot be expressed as a whole number or the ratio of two whole numbers. What the Pythagoreans had discovered were IRRATIONAL NUMBERS! Agony!
4. The discovery of irrational numbers greatly disturbed the Pythagoreans. Irrational numbers had no place in their philosophy of the universe. They believed everything could be described in mathematical certainty. With irrational numbers, there is no certainty. It cannot be expressed rationally. You might think, “Big deal! Get a life, you Pythagoreans!” However, once the Pythagoreans found something they couldn’t be certain about, they started to worry whether they were truly certain about anything! What if all their theories were wrong? What if their view of the universe was wrong? Very upsetting stuff.

C. Euclid and His Elements (365 – 300 B.C.)

  

1. Euclid was a mathematician and teacher in Alexandria. He wrote a book called The Elements. In it, Euclid beautifully encapsulated the knowledge of geometry by Greeks before his time, and he added many theorems of his own. The Elements is the basis for modern geometry.
2. Here is a classical arithmetical problem from Euclid. It is a conversation between a mule and a donkey. The mule says to the donkey, “If you gave me one of your sacks, I would have as many as you.” The donkey replies, “If you gave me one of your sacks, I would have twice as many as you.” How many sacks to they have? … The answer is five for the mule and seven for the donkey. ( x+1=y-1 and 2(x-1) = y+1 )

VII. Numbers That Fascinated the Ancients

A. Pi (Î ) – Pronounced Pie

  

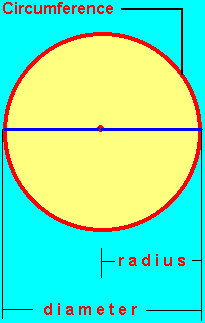
1. The irrational number pi (3.14…) has been known about for thousands of years. The Babylonians calculated pi to be 3.125. Independently, the Egyptians discovered pi and calculated it to be 3.1605.
2. The ancients were probably fascinated with the properties of circles. It became apparent that no matter what size a circle was, its circumference was always a little more than three times its diameter. In other words, take any circle, and divide its diameter into its circumference, and you will get the number pi. Around 250 B.C., the Greek mathematician Archimedes calculated pi to be 3.14. He was the first to calculate it with reasonable accuracy.

B. Phi – Pronounced Fie

  

1. Phi is also an irrational number calculated as 1.618… and has many unusual properties. It is known as the Golden Ratio because of its uniqueness. For example, if an architect builds a building with its different parts corresponding to the phi ratio, the building will be visually pleasing. Phidias, (500 – 432 B.C.) a Greek sculptor who worked on the Parthenon in Athens, applied phi when making his sculptures. Some scholars believe phi may have been used in the design of the pyramids at Giza.
2. Interestingly, the dimensions of the Ark (large chest) of the Covenant were said be in terms of phi, and Noah’s Ark (large ship) was said to have dimensions in terms of phi.
3. Plato believed phi to be the key to physics and the cosmos.
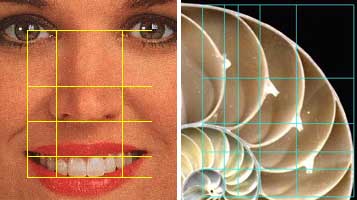
4. Surprisingly, phi is found in some aspects of nature. For example, seeds in a flower are arranged according to phi. The spirals in some sea shells are arranged according to phi. Finally, Dr. Stephen Marquardt, a self-described expert in beauty, believes that the more the proportions of a person’s face relate to phi, the more attractive that person will be to others.

C. How Can You Find Phi?

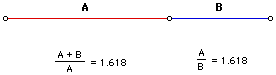
1. Take a line segment, and divide the segment into two parts: line segment A and line segment B. Line segment A must be longer than B. If you add segments A and B, and divide that sum by segment A, you get phi. Also, if you divide line segment A by segment B, you’ll get phi. So, A+B/A = phi and A/B = phi. (Notice that ratios have been created.)

D. Perfect Numbers

1. A perfect number is a whole number, greater than zero, and when you add all the factors of that number, (not including itself) the result should be that number. For example, take the number six. The factors of six are one, two, three, and six. Now add all the factors except six. One plus two plus three is six, so six is a perfect number.
2. Pythagoreans are the mathematicians to coin the name “perfect number”. They believed perfect numbers had mystical properties.

BUT MYSTICAL PROPERTIES WILL HAVE TO BE DESCRIBED BY MYSTICS.